기록: UCL Course on RL 요약 및 정리 (Lecture 10: Classic Games and Minimax Search)

This post covers not only Lecture 10: Classic Games (davidsilver.uk) but also:


Lecture Goal
  • 체스나 바둑 등 고전적인 대전 게임을 푸는 minimax search 기법을 배운다. 또한 minimax search를 reinforcement learning에 녹여 통합적으로 푸는 방법을 배운다.

Game Theory
  • Best response
    • In game theory, the best response is the strategy (or strategies) that produces the most favorable outcome for a player, taking other players' strategies as given.

    • Assume that other players become parts of the environment.
    • Then, the game is reduced to an (single-agent, stationary-environment) MDP for \(i\)-th agent.
    • Best response is the optimal policy for the MDP.
    • Therefore, the best response is a solution to a single-agent RL problem.
  • Nash equilibrium
    • Imagine that each player is told the strategies of the others. Suppose then that each player asks himself: "Knowing the strategies of the other players, and treating the strategies of the other players as set in stone, can I benefit by changing my strategy?"
    • If any player could answer "Yes," then that set of strategies is not a Nash equilibrium. But if every player prefers not to switch (or is indifferent between switching and not), then the strategy profile is a Nash equilibrium. 
    • Thus, each strategy in a Nash equilibrium is the best response to the other players' strategies in that equilibrium.

    • Self-play RL
      • Suppose that an experience is generated by playing games between virtually multiple agents:
        • \(a_1 \sim \pi^1, a_2 \sim \pi^2, \cdots \)
      • 예를 들어, agent 1은 자신이 뽑은 action을 제외한 모든 다른 action에 의한 state transition은 마치 environment가 state를 변경한 것처럼 보인다.
      • Consider a joint policy \(\pi = \left \langle \pi^1,\pi^2,\cdots,\pi^n \right \rangle\).
      • 이 joint policy 하나를 통째로 운용하는 agent를 self-play RL agent라고 한다. 일반적인 RL은 reward를 최대화하는 policy 하나를 찾지만, self-play RL은 두 policy가 서로 상충하는 setting이다.
    • Nash equilibrium is a fixed-point of self-play RL.
      • Joint policy가 Nash equilibrium에 있다는 것은, joint policy가 더 이상 향상되지 못한다는 뜻이다 (cf. no player would choose to deviate from Nash).
  • Two-player zero-sum games
    • In this lecture, we will focus on a special class of games:
      • A two-player game has two (alternating) players.
        • Called white and black (e.g., Chess and Go)
      • A zero-sum game has equal and opposite rewards for black and white.
        • \(R^1+R^2=0\)
        • 체스나 바둑에서는 오직 한 명 만이 승자. 상대가 승자라면 나는 패자가 될 수 밖에 없는 게임.
    • We consider methods for finding Nash equilibria in these games.
      • Minimax search (i.e., planning)
      • Self-play reinforcement learning (joint policy를 운용하는 RL)
    • There is a unique Nash equilibrium for TPZS games.
  • Perfect and imperfect information games
    • A perfect information game is fully observed.
      • Chess 
      • Checkers 
      • Othello 
      • Backgammon 
      • Go
    • An imperfect information game is partially observed.
      • Scrabble (영어 학원에서 하던 단어 맞추기 게임)
      • Poker

Minimax Value and Policy
  • Goal: finding Nash equilibria in a two-player zero-sum game
    • 무작정 reward를 최대화하는 RL과는 약간 다르다.
    • 상대가 나만큼 똑똑하다는 가정하에, 서로의 승리를 방해하면서 상호 발전한다면 어떤 policy에 도달할까를 찾는 문제다.
  • Value function for a joint policy
    • \(v_{\pi}(s) = \mathbb{E}_{\pi}[G_t|S_t=s]\)
    • = the expected total reward given a joint policy (white가 이기면 reward +1, black이 이기면 reward -1 등)
  • Minimax value function
    • Suppose that an experience is generated by playing games between two alternating players:
      • \(a_1 \sim \pi^1, a_2 \sim \pi^2, a_3 \sim \pi^1, a_4 \sim \pi^2, \cdots \)
    • \(v_{*}(s) = \underset{\pi^1}{\max}\underset{\pi^2}{\min}v_{\pi}(s)\)
    • = (converged) value function where white maximizes white's expected return while black maximizes black's expected return (음수 return은 black의 승리를 의미)
    • = (converged) value function where white maximizes white's expected return while black minimizes white's expected return (zero-sum property)
    • = minimizing the possible loss for a worst case (maximum loss) scenario
    • Note: 상식적으로 두 플레이어는 매 state에서 자신의 return이 높아지는 쪽으로 플레이할 텐데 (best response), zero-sum 게임에서는 자신의 return이 높아지게 하는 것과 상대의 return이 낮아지게 하는 것이 동치이기 때문에, minimizing the possible loss for a worst case (maximum loss) scenario 하는 게 Nash equilibrium이다.
  • A minimax policy is a joint policy that achieves the minimax values.
    • 물론 minimax policy가 아니라 두 player가 각자 다른 전략으로 게임에 참여할 수도 있고, 그 때는 value function은 minimax value function이 아니라 그냥 value function for a joint policy가 된다.
  • There is a unique minimax value function.
  • \(\Rightarrow\) Minimax policy로 수행하는 (with exhaustive searching) two-player zero-sum 게임은 Nash equilibrium에 있다.
  • Minimax - Wikipedia
    • In two-player zero-sum games, the minimax solution is the same as the Nash equilibrium.
    • Minimax is used in zero-sum games to denote minimizing the opponent's maximum payoff. In a zero-sum game, this is identical to minimizing one's own maximum loss, and to maximizing one's own minimum gain.
    • In non-zero-sum games, maximizing one's own minimum payoff is not generally the same as minimizing the opponent's maximum gain, nor the same as the Nash equilibrium strategy.

Minimax Search
  • Assume an exhaustive searching
  • Minimax values can be found by depth-first game-tree search:

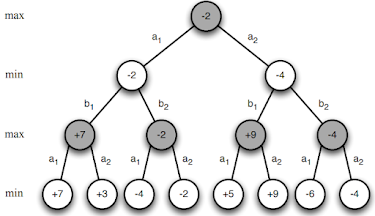
  • 그림에서 leaf node가 end-game state라고 치자. 두 player가 minimax policy로 플레이 하고 black이 먼저 수를 둔다면, 마지막 state의 직전 state에서 black은 무조건 자신이 얻을 value가 높아지는 걸 택할 것이다 (즉, 왼쪽부터 순서대로 \(v_{*}=7,-2,9,-4\). 그 이전 state에서는 white가 무조건 자신의 얻을 value가 높아지는 걸 택할 것이다 (best response). Zero-sum game이므로 이는 black이 얻을 value가 낮아지는 쪽을 택하는 것과 같다 (minimax). 이런 절차로 black의 현재 state에서의 (minimax) value를 구하면:

  • 즉, 승부는 이미 black의 패배로 결정났다.

Drawbacks of Minimax Search
  • Search tree grows exponentially
  • Impractical to search to the end of the game

Minimax Search with Value Function Approximation
  • Instead, use (minimax) value function approximator \(v(s, w) \approx v_{*}(s)\)
    • E.g., binary feature vector (장기말의 생존 유무 등) with linear weighting
    • Note: 아직 learning은 아니기 때문에 이 weight는 search 과정에서 학습하는 게 아니라 고정. Hand-crafted value function (no learning).
  • Minimax search run to a fixed depth
  • Use value function to estimate minimax value at the depth
  • Example: Deep Blue
    • 8000 handcrafted chess features
    • Binary-linear value function
    • Weights are largely hand-tuned by human experts.
  • 현실에서는 Alpha-beta pruning 등을 이용하여 tree의 branch 중 굳이 탐색할 필요없는 branch를 삭제하는 식으로 search space를 더욱 줄인다.

Learning with Minimax Search
  • Why don't we learn the value function approximator?
  • 위 value function approximator의 성능을 게임이 진행함에 따라 발전시키는 게 자연스러운 아이디어 확장이다. 
  • \(\Rightarrow\) self-play RL

Self-Play Reinforcement Learning
  • Classic game은 rule이 이미 정해져 있다. 따라서 일종의 known MDP이다. 따라서 model-based RL에서 simulation-based planning을 하여 data augmentation 효과를 내는 것처럼 실제로 (예를 들면) 체스 대국 도중에 스스로 self-play해서 전략을 도출할 수 있다.
  • 1. 일단 value function approximator을 학습한다. (learning)
  • 2. 그 후 minimax search with VFA를 통해, 일정 depth(시간) 미래의 state의 (approximated) minimax value를 근거로 action을 선택한다. (searching)
  • Note: Sarsa revisited
  • Define \(v(s, w) \approx v_{*}(s)\)
  • Policy improvement
    • For deterministic games, \(q(s,a) = v(s')\) since \(s'\) is deterministic given \(s, a\). Let's define such mapping as \(s' =succ(s,a)\).
    • \(\pi^1(s) = \underset{a}{\mathrm{argmax}} \; v(s'=succ(s,a), w)\)
    • \(\pi^2(s) = \underset{a}{\mathrm{argmin}} \; v(s'=succ(s,a), w)\)
    • Greedy for each player
  • Value function or value approximator update: MC, TD(0), TD(\(\lambda\)), etc.

    • 하던대로 하면 됨
  • Minimax search with VFA
    • Minimax search run to a fixed depth
    • Use the value function approximator to estimate minimax value at the depth

Combining Reinforcement Learning and Minimax Search
  • Monte Carlo Tree Search같은 simulation-based search를 model-based RL에서 이용했던 것처럼, minimax search를 RL에 이용하여 좀 더 의미있고 똑똑한 방식으로 value를 추정해보자.
    • 다만 minimax search는 정말로 가능한 branch를 (특정 depth까지) 다 탐방해보고, simulation-based search는 sampling을 통해 일부 branch만 탐방한다는 차이점이 있다. 
  • 위의 TD(0) 알고리즘은 value approximator 학습 초기에는 \(v(S_{t+1}, w)\)가 굉장히 의미없는 값일 가능성이 높다. Minimax policy가 Nash equilibrium인 걸 알기 때문에 search를 통해 좀 더 전략적으로 value function approximator를 update할 필요가 있다.
  • 가정: deterministic game
  • TD root
    • Define: \(l_{+}(s)\) is the leaf node achieving minimax value from \(s\).
      • Minimax search with VFA의 경우처럼, \(s\)에서 minimax policy로 tree search를 진행할 때 tree의 최대 깊이 앞(미래)에 있는 node
      • (exhaustive search 불가능하므로 미리 tree의 최대 깊이를 특정해둠)
    • Take initial action: minimax policy와 \(v(S_{t+1}, w)\)에 따라 \(S_{t+1}=s_{t+1}\)을 실제로 택한다 (또는 \(\epsilon\)-greedy 등 적절히 exploration을 위한 randomness를 추가하여).
    • Value function backed up from search value (kind of simulation) at next state:
      • \(v(S_t,w) \leftarrow v(l_{+}(S_{t+1}),w)\)
    • Search tree depth를 2로 설정한 TD root algorithm 예:
    • Note: 왜 \(S_{t+1}\)의 value는 무시하고 그보다 더 미래의 state의 approximated value로 backup을 하는지 궁금할 수 있는데, 실제로 minimax policy를 적용해서 미래 state \(l_{+}(S_{t+1})\)를 찾은 것이므로, 이상적으론 \(l_{+}(S_{t+1})\)의 true minimax value나 \(S_{t+1}\)의 true minimax value나 실은 같은 것이어야 한다 (아래 minimax search 예시 그림 참고). TD root는 \(v_{*}(S_{t+1})\)를 더 잘 근사하는 게 \(v(S_{t+1},w)\)보단 \(v(l_{+}(S_{t+1}),w)\)라고 가정하는 것이다.
  • TD leaf
    • TD root에서는 \(v_{*}(S_{t+1})\)를 더 잘 근사하는 게 \(v(S_{t+1},w)\)보단 \(v(l_{+}(S_{t+1}),w)\)라고 가정했다. TD leaf는 한 발 더 나아가, \(v_{*}(S_{t})\)를 더 잘 근사하는 게 \(v(S_{t},w)\)보단 \(v(l_{+}(S_{t}),w)\)니까 \(v(l_{+}(S_{t}),w)\)를 업데이트하자 제안한다.
    • \(v((l_{+}(S_t),w) \leftarrow v(l_{+}(S_{t+1}),w)\)
  • TreeStrap
    • TD root와 TD leaf에서는 minimax policy와 \(v(S_{t+1}, w)\)에 따라 \(S_{t+1}=s_{t+1}\)을 일단 택하고 (real play) update를 어떻게 할지 고민했다 (search).
      • TreeStrap은 search에 집중한다.
    • 또한, TD root와 TD leaf는 minimax search 이후 오직 하나의 node만 update했다. 
      • TreeStrap은 minimax search로 방문한 모든 노드를 업데이트한다.
    • 현재 노드 \(S_t\)와 그의 모든 자식 노드 \(s\)에 대해 (특정 depth까지, leaf node를 제외한),
      • \(v(s,w) \leftarrow v(l_{+}(s),w)\)
    • TreeStrap에서 현재 노드를 root로 (특정 depth까지) minimax search를 한 뒤 search tree의 모든 노드의 value를 업데이트하는 모습:
    • Note: TD leaf는 현재 state에서도 self-play를 통해 \(v_{*}(S_{t})\)를 추정해야 하고, action sampling을 해서 얻어진 다음 state에서도 self-play를 해서 \(v_{*}(S_{t+1})\)를 추정해야 한다. 그 후 이 두 값을 가중치 합해야 한다. 이는 두 가지 self-play (uncertainty)를 동시에 취하는 거라 불안하다. 또 게임 초반에는 value approximator가 상당히 부정확하므로 action sampling해서 다음 state의 정보로 backup하는 게 불안할 수 있다. TreeStrap은 그런 문제 의식에서 출발했다.

Monte-Carlo Search and MC Tree Search in Games

Reinforcement Learning in Imperfect-Information Games
  • Imperfect-information games: Blackjack





  • 상대방의 action, state를 제대로 알 수 없는 imperfect game의 경우, UCT 단순한 MCTS를 쓰면 Nash equilibrium을 찾을 수 없다. 수렴하지 않는다. 따라서 모든 적의 average behaviour를 학습한 뒤 이에 대한 best response를 도출하여 gradient smoothing 같은 효과를 낸다 (매 update의 노이즈를 줄인다고 생각하자). 따라서 일반 UCT보다 강건하다.

댓글

댓글 쓰기

이 블로그의 인기 게시물

기록: UCL Course on RL 요약 및 정리 (Lecture 6: Value Function Approximation)

이미지
This post covers  Lecture 6: Value Function Approximation (davidsilver.uk)   The entire course materials can be found on the following page:  Teaching - David Silver . Lecture Goal Learn how to deal with a large-scale (potentially continuous) state space with RL Learn value function approximation Learn Deep Q-Network (DQN) and batch methods Credit:  Find order of polynomial approximation and LeastSquares for given datapoints Value Function Approximation Lookup table Table store an entry for each lookup index. Value-state Index = \(\forall s \in S\), where \(S\) is a finite and discrete state space Entry = \(V(s)\) Action-state Or every state-action pair \(s, a\) has an entry \(Q(s,a)\) Or every state \(s\) has entries \(Q(s,a)\) for all actions \(a \in A\) So far, we have represented a value function by a lookup table. Large MDPs Memory inefficiency : too many states or actions to store in memory Too slow to learn the value of each state individually Note: neighboring states might st
자세한 내용 보기

기록: UCL Course on RL 요약 및 정리 (Lecture 9: Exploration and Exploitation)

이미지
This post covers not only  Lecture 9: Exploration and Exploitation (davidsilver.uk)  but also : 'Reinforcement Learning' 카테고리의 글 목록 (yjjo) The Multi-Armed Bandit Problem and Its Solutions (lilianweng.github.io) Bayesian Bandits - Thompson Sampling (tistory.com) The entire course materials can be found on the following page:  Teaching - David Silver . Lecture Goal MDP를 풀 때 exploration과 exploitation 중 어느 한 쪽만 사용하면 optimality에 도달하지 못한다 (trade-off). 본 강의에서는 둘 사이의 균형을 맞추는 알고리즘을 소개한다. Credit: UC Berkeley Intro to AI course lecture 11 Takeaway Use (Bayes-) UCB algorithms Exploration vs. Exploitation Dilemma Exploitation: make the best decision given current information E.g., go to your favorite restaurant Exploration: gather more information E.g., try a new restaurant Dilemma The best long-term strategy may involve short-term sacrifices and risks How does an agent obtain enough information to make the best overall decisions with the lowest sacrifices? [In-A-Nutshell] Key Principles an
자세한 내용 보기

KAIST 회고 (1): 공부법 정리

이미지
(2021-08-29 초안 작성) 성적을 잘 받기 위한 기본 정리 1: 시험과 과제 마감일은 우리를 기다려주지 않는다 내용) 오늘 들은 강의는 이틀 내에 복습하라 해설) 엘리베이터 앞에 몇 초만 늦게 도착해도 먼저 엘리베이터에 타고 올라간 사람보다 많게는 수 분 가량 늦을 수 있다. 학교는 학생의 학습 능력을 매 초 마다 연속적으로 체크하지 않는다. 억울하지만, 시험 당일이나 과제 제출 당일에 퍼포먼스를 제대로 못 보여주면 그 후폭풍은 거대하다. 예를 들어, 한 학기 동안 매번 당일 수업 내용으로 다음 날 시험을 보는 상황을 가정하자. 매일 복습을 하는 학생과 항상 수업 이틀 뒤에 복습을 하는 (즉, 시험치고 다음 날) 학생이 있다면, 해당 학기가 끝난 뒤 두 학생의 이해도는 별반 차이 없을 것이다. 둘 다 공부를 제대로 했다는 가정 하에, 복습을 며칠 미룬다고 큰 차이가 날 리가. 다만 시험 성적은, 앞의 학생은 충분히 높을 것이고, 뒤의 학생은 비교적 낮을 것이다 (수업을 듣자마자 모든 걸 깨닫지 않는 이상). 이 예시에서 두번째 전략을 취한 학생은 매우 억울할 것이다. 그러나 이게 현실이다. 시험은 '당일까지'의 이해도를 측량한다. 과제도 마찬가지다.  현실에서는 시험이나 과제 전까지 충분히 시간을 주지 않느냐 반문할 수 있다. 그러나 매 강의는 시간 의존적이다. 오늘 듣는 강의는 필연적으로 지난 수업 일이나 저번 주, 심지어 선수 과목의 내용과 밀접한 연관이있다. 따라서, 당연히도, 오늘 들은 강의 내용을 다음 수업일까지 복습하지 않는다면, 다음 수업일의 강의 내용을 이해하는 게 매우 힘들어지고, 수업 시간에 제대로 이해하지 못하니 복습할 내용과 다시 공부할 내용은 눈덩이처럼 불어난다. 더 심하게는, 수업 시간에는 하나도 이해 못하고 시간을 날린 뒤, 방에 돌아와서 당일 강의록을 보면서 스스로 처음부터 공부해야 할 수 있다. 실제로 KAIST에서도 많은 학생들이 이런 식으로 공부하면서 강의 하나를 이해하는 데에 드는 시간을 두 배 혹은 그
자세한 내용 보기